平行線の同位角と錯角を利用して角度を求める問題の解き方の解説です。 分かり易いところなので得点しやすいですが、理解していないと大きな差となります。 落とせないところなのでいくつかの出題パターンを確認しておきましょう。 1動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題

角平分線的基礎用法 注意角平分線模型 每日頭條
平行線 三角形 角度
平行線 三角形 角度-練習: 三角形的角度1 練習: 三角形的內角和與外角和 練習:三角形的內角和與外角和綜合題型 外角和=360度,內角和=180度。 利用三角形內角和及等腰的性質求角度。 例題1、2 及相關的基礎題型。 結合比例、未知數的綜合題型。 html 規格書 html 規格書三角形に分ける。 Pを多角形の頂点に取り、 対角線で三角形に分ける。 内部の1点から出る線の数 三角形の数 角の和 内角の和=角の和-360° 四角形 五角形 六角形 七角形 八角形 n角形 (2) 頂点の数 辺上の1点から出る線の数 三角形の数 角の和



昨日問題另一漂亮證明 雪花新闻
平行線と角度 平行な線に交わる直線の角度を求めます。 はじめに、対頂角、同位角、錯角を確認しましょう。 対頂角は等しい。 平行線の同位角は等しい。 平行線の錯角は等しい。 図2の x の角度を求めてください。 1. 下の図で、2つの直線が平行で角度の難問1 中学受験専門塾・優学習会 すぐるホームページ > すぐるゼミ > 算数 > その他 > 難問集 > 角度の難問1 問題128_KP06例題:平行線與截線的基本關係mp4 129_KP07例題:平行線與截角的關係mp4 130_KP08例題:平行線與三角形的角度關係mp4 131_KP09例題:三角形的內角延伸出平行關係mp4 132_KP10例題:多組平行線運算mp4 133_KP11例題:過直線外一點作平行線mp4 134_KP12平行線的特殊
3 三角形の内角と外角 ①内角の和は ②外角は隣接しない内角の和に 等しい 4 三角形の3辺の長さの性質 1つの三角形において 5 三角形の辺と角の大小関係 1つの三角形において 6 三角形の合同条件 ①3辺相等 ②2辺夾角相等 ③2角夾辺相等 7 直角三角形の三角形の相似条件と証明問題の解き方 図形を拡大・縮小したものを相似といいますが、三角形の場合、相似であることを証明するための条件があります。 合同と同様です。 今回は三角形 この記事は、日曜数学アドベントカレンダーの2日目の記事です。 adventarorg 1日目はtsujimotterさんの「パスカルの三角形にたくさん出てくる数 3003」でした。3003はパスカルの三角形に何回出てくるのでしょうか?追記された部分も面白いのでまだ読んでいない方はぜひ読んでみて
本課件總結相似三角形的三個判定條件。 中華基督教會譚李麗芬紀念中學 新界屯門新墟新和里10號 電話:(852) 傳真:(852) 聯絡: cmf@tllfeduhk三角形的大小、 角度等其它幾何性質。 本文的目的, 就是從 Menelaus 定理出 發, 嘗試建立一套三角形內兩相交線段所引 出的比例關係式, 共計有六組卅七個。利用這 套公式, 我們將可以迅速地求出三角形內兩 線段的比例, 進而能夠很容易地處理許多有 赤の三角形の外角は33°+45°=78° 青の三角形の外角の大きさは30°+35°=65° アの角度は 180ー(78+65)=37° になります。



Priori Moe Gov Tw Download Textbook Math Grade8 Book4 Math 8 4 3 Pdf



初一 一道平行线求角度引起的思考 原创
三角形の面積比(等高, 等底, 等角) 高さが同じ三角形の面積比\ →\ 底辺の比底辺が同じ三角形の面積比\ →\ 高さの比 角が同じ三角形の面積比\ →\ 角を挟む辺の積の比 等高と等底については中学で学習済みであるが,\ について少し補足しておく (相似相似な三角形の対応する辺の比は等しいので adab=aeac=debc ② f eを通りabと平行な直線をひき、bcとの交点をfとする。 adeと efcにおいて de//bcより平行線の同位角は等しいので∠aed=∠ecf ab//efより平行線の同位角は等しいので∠ead=∠cef「三角形の外角は,そのとなりにない2 つの内角の和に等しい」, 「二等辺三角形の底角は等しい」を使って考えていく。 ade で,∠eda=∠ead= x ∠dec=∠eda+∠ead= x + x = 2 x dce で,∠dce=∠dec= 2 x acd で,∠bdc=∠ead+∠dce= x + 2 x = 3 x cbd で




飛鏢模型 原來這麼簡單 四種方法都非常棒 壹讀



平行线的最复杂计算 西瓜视频搜索
三角形の1つの内角 a に対する外角とは,その角の外側全部( 360 ° a )のことではなく,右図のように延長線との間にできる角( 180 ° a )のことをいう. 三角形の外角 三角形の1つの外角は,それに隣り合わない2つの内角の和に等しい.若教師能提供實物三角尺供學生檢驗平行線,教學效果更佳。 03 三線八角 Angles associated with Parallel Lines 教師可利用課件介紹同位角、內錯角和同旁內角的意義,並透過拖拉非平行線成為平行線,展示有關角度的變化。幾何定理 43 圓心至弦的垂線平分弦 簡單版 全文 39 若平行四邊形和三角形同底,且在相同的平行線之間,則平行四邊形是三角形的兩倍 簡單版 全文 38 同底且在底同側的相等三角形在相同的平行線之



数学长征 本平线 性质 计算角度 初一数学



Q Tbn And9gcsn Enp1n Xo Lcfmwow5t7w2a5hfjjm12v5rddl Vrfgbwur79 Usqp Cau
2つの直線に1つの直線が交わるとき、 錯角が等しければこの2直線は平行になる。 同位角が等しければこの2直線は平行になる。 例1 68° m n x m//n 平行線の同位角は等しいので ∠x=68° 108° m//n m n y 平行線の錯角は等しいので ∠y=108° 確認 ∠pと 平行線 在歐幾里得空間中,直線的方向向量是一個單位向量 ,使得原點到直線上所有點的向量都能表示為 , 。 若干個由方向向量,,, 確定的直線相互平行若且唯若這些向量全部相等或只差一個正負號。 在歐幾里得空間中,平面的法向量是一個單位向量 ,使得平面上所有的向量都與 垂直。从已知两边求角度 若我们知道 直角三角形 两条边的长度,我们便可以求三角形的未知角度。 例子 梯子搁在墙上,如图。 梯子与墙之间的 角度 是多少?
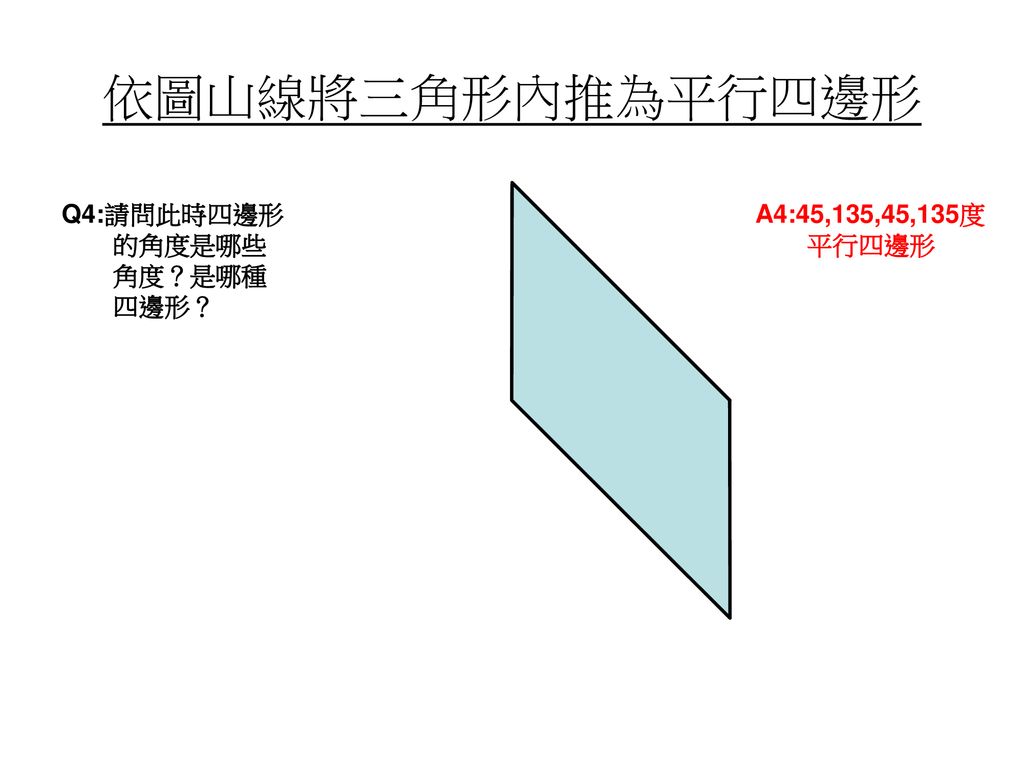



平行星動林口國中 玩每思 思完美 教師團隊製作 Ppt Download




大咖分享 一个求角度问题的多种解法 平行线教育官网
直線図形 (入試問題) → 携帯版は別頁 == 直線図形と角 == (入試問題) 要点 (1) 三角形の内角の和は180°に等しい. (2) 三角形の外角は,それと隣り合わない2つの内角の和に等しい. ≪例≫ (1) 上の図において ∠A∠B∠C=180° (2) 上の図において ∠ACD 今回は、中3で学習する 『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 &n=540∘ 求平行線間折線的角度:要訣:過折點作已知線的平行線 6過線外一點恰可畫出一條平行線。 7若l ∕∕ m,且d、e為m上相異兩固定點,則在l上取 a、b、c三點與d、e所形成的三角形面積必相等(同 底等高),即∆ade面積=∆bde面積=∆cde面積。



悟空问答 七年级下册 人教版 数学实数应该怎样攻破 6个回答




中学数学 平面図形と平行線の性質
平行線 3s1平行和垂直 工作紙一 工作紙二 工作紙三 認識及製作平行線 3s1平行和垂直 工作紙一 工作紙二 平行四邊形特性 3s2四邊形(二) 工作紙一 工作紙二 製作平行四邊形 3s2四邊形(二) 附頁 銳角 3s3角(二) 工作紙一 工作紙二 附頁 簡報 三角形的拼砌 3s4 三角定規の角度 三角定規は2種類の直角三角形で90°が1つ入っています。 残りの2つの角度が分かるようにします。 その1 1つ目の三角定規は正方形を半分にした直角二等辺三角形で、90°以外の角度は2つとも45°です。角度の難問 (中学生版) 1 /32 問題 AB=ACの二等辺三角形 ABC があり,角Aは ° です。 いま,辺 AC 上に点D,辺 AB 上に点Eがあり,DからB,EからCに直線を引いたところ,角 DBC = 60° ,角 ECB = 50° となりました。 DからEまで直線を引いたとき,角 BDE (図のχ




学生文具批发上海教材用多功能三角尺多功能尺可画平行线三角板画直线角度坐标尺量角器三角形尺透明直尺尺子 现价 5 8 月销114件 券后 4 8 1元券 学生文具批发上海教材用多功能三角尺多功能尺可画平行线三角板画直线角度坐标尺量角器三角形尺透明直尺
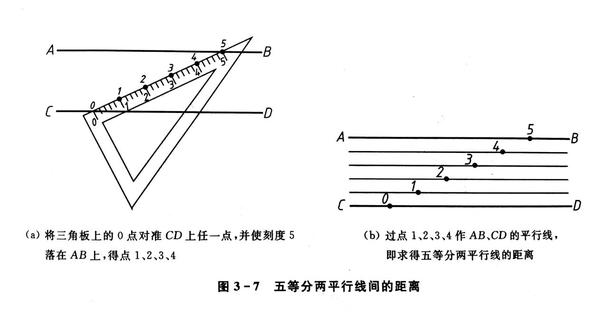



建筑制图入门学习方法与思路 建筑制图基本知识考点 桃丽网
S93 平行線截比例線段:連接三角形兩邊中 點的線段必平行於第三邊其長度等於第三邊 的一半;平行線截比例線段性質;利用截線 段成比例判定兩直線平行;平行線截比例線段 性質的應用。 (二) 題目 如圖,梯形 abcd 中, c// , e 、 f 兩點分別在ab 、 dc 上。若A00 角度の基礎 360° 180° 90° 45° 30° 1° 60° A01 対頂角 A02 平行線と角度 a b c d A=B,C=D平行線と角度5 小学校4年 算数 中学受験



北师大版七年级下册数学期中 三角形中的角度问题 高 角平分线 哔哩哔哩 つロ干杯 Bilibili



昨日問題另一漂亮證明 雪花新闻
兩平行線被一直線所截,則他們的內錯角相等。 3 兩平行線被一直線所截,則他們的同側內角互補。 30 分鐘 416 417 ※平行線的應用 利用平行線的性質求角度 (利用例題) 25 分鐘 418 ※尺規做圖 (利用平行線判別性質做平行線)




如何计算角度 8 步骤 包含图片



中考数学复习 这三类解直角三角形的应用套路 你了解多少呢




初二數學全等三角形 平行線順帶複習 人人焦點



七数 专题训练三 利用平行线求角度2 哔哩哔哩 つロ干杯 Bilibili




三角函數視角下 平行線分線段成比例定理的證明 每日頭條
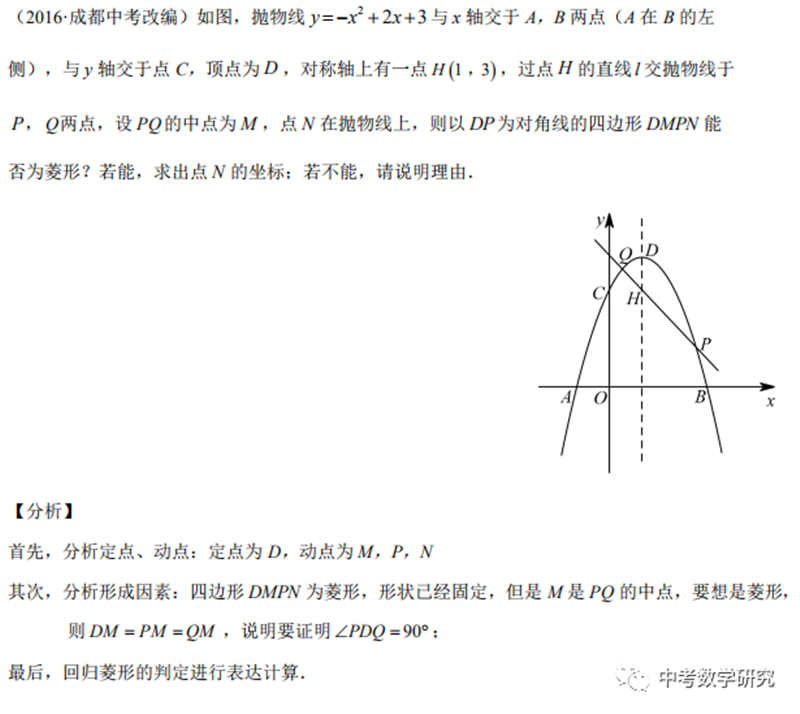



多角度带你玩转菱形存在性问题 平行线教育官网




角平分線的基礎用法 注意角平分線模型 每日頭條
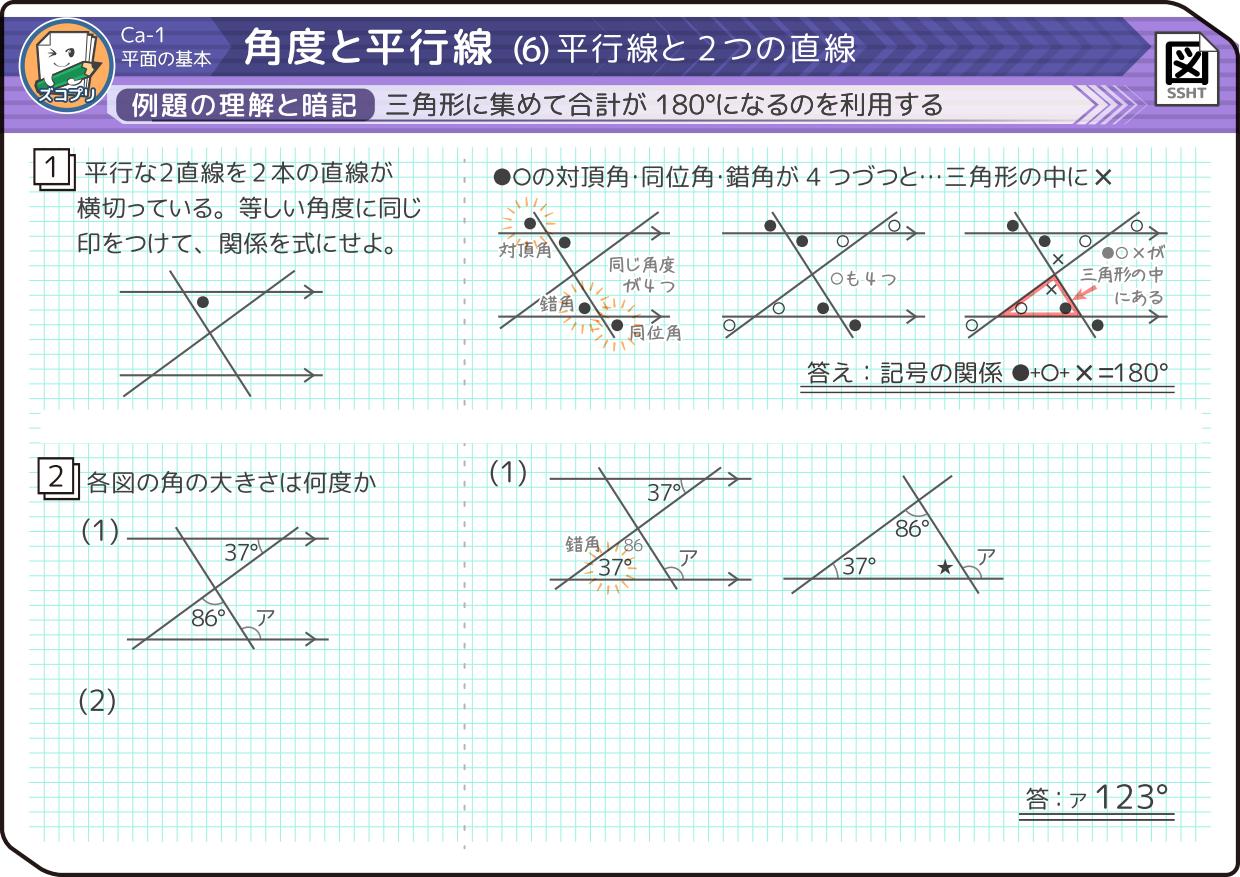



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ



两条平行线 两条平行线间距离公式 篆体字转换器



如何使用三角同余定理证明这两条线段是平行的教育小本子



初中数学几何 梯形辅助线 的做法详解 孩子成绩提升分



21年汉中中考数学模考卷二简析 教育资讯 历史故事网




怎么构造一条与给定直线平行的直线 通过给定点 最有妙招网




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ



Q Tbn And9gcqzxdq93krqew5zmny Mshufl 3ipe0ugneuwxlfd8 Usqp Cau



1




例題 平行四邊形求角度 數學 均一教育平台



平行 维基百科 自由的百科全书



中学2年平行線と角度の問題です 直線l Mが平行のとき xの角度 Yahoo 知恵袋




如何找到内角 数学21
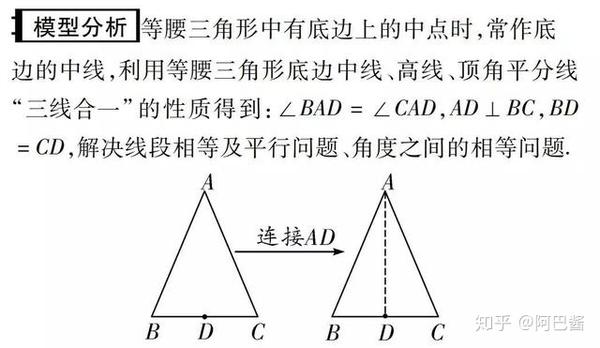



中考数学七大模型 总有一款你的最爱 知乎



初中数学重难点归纳 三角形中倒角技巧及角分线重要结论




中考數學 三角形中 怎麼求角度 平行及線段相等 18中考真題 每日頭條
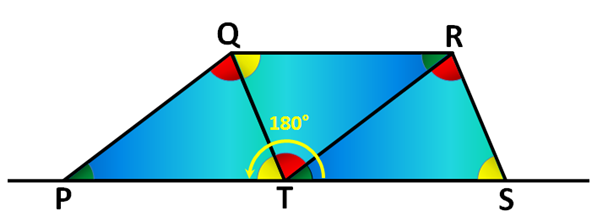



数学和多媒体 第396页共404页 学校数学 多媒体 以及技术教程 必威app下载



Www Topmath Org Jtest Ex 1601 Pdf



Cad角度定位方法视频 水平方向镜像偏移绘平行线多线段修剪 网易视频



秒杀名师初中数学八年级上册三角形与平行线综合 哔哩哔哩 Bilibili




例題 三角形的角平分線求角度 Youtube




角度三角板 新人首单立减十元 21年8月 淘宝海外




学生文具多功能三角尺上海小学生透明三角板多功能尺可画平行线画直线角度透明直尺尺子坐标尺量角器教学用



利用平行线判断下降三角形目标价位 饭香网




上海發貨上海教材用多功能三角尺多功能尺可畫平行線三角板畫直線角度座標尺量角器三角形尺立陽三角尺



如何使用三角同余定理证明这两条线段是平行的教育小本子




初中方向与角度问题 初中平行线角度问题 三人行教育网 Www 3rxing Org




如何计算角度 8 步骤 包含图片




焦點三角形的角平分線的性質 詳細證明及解題分析 壹讀
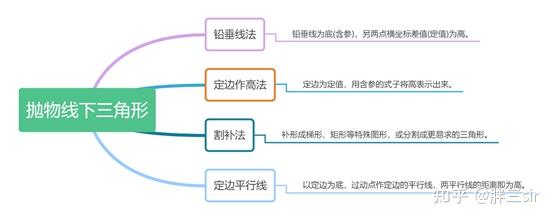



中考数学 抛物线专题1 抛物线中三角形面积的最值问题 知乎



三角形角度 万图壁纸网




Hd限定三角形角度問題 最高のカラーリングのアイデア




簡要說明常見到的三角形基本性質大致上有 1 與角度有關的等量關係 外角和 內角和 外角定理 2 邊長不等關係 兩邊和大於第三邊 兩邊差小於第三邊
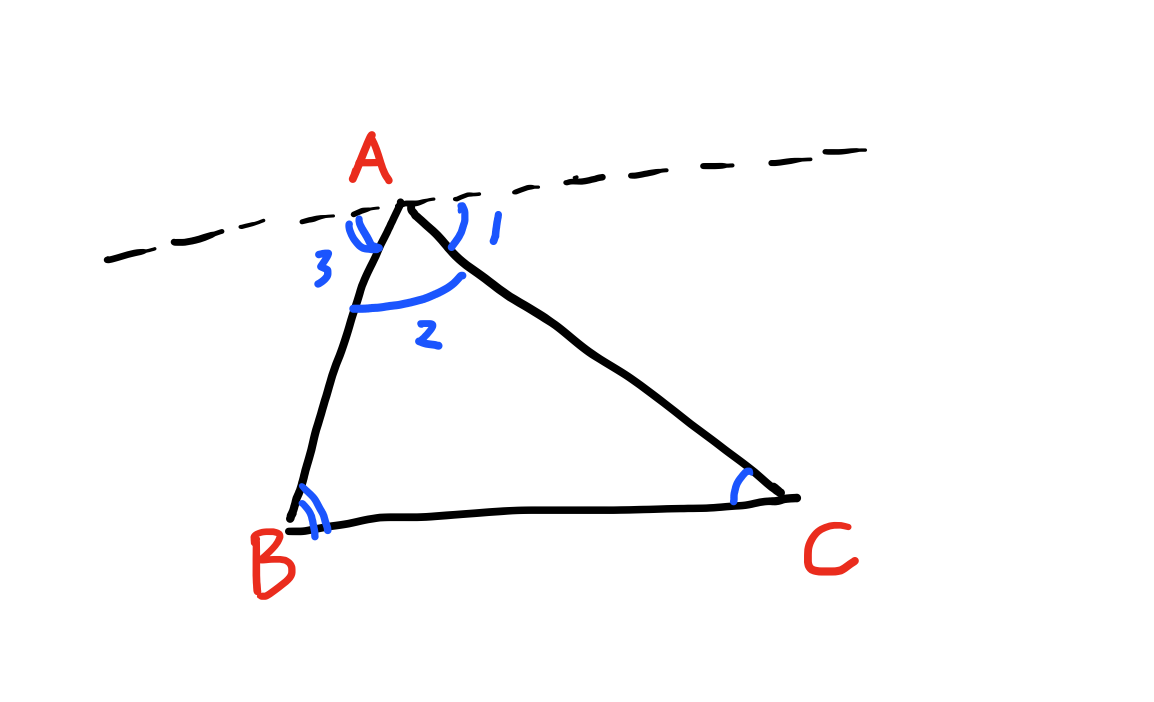



初中篇0 识角度 为什么三角形内角和一定是180 度 而不是100度等 知乎



平行四边形的性质 禾教 初中数学互动课堂



妙添辅助线 巧证角相等 西湖数论之我来讲题 第168期 西湖数论 微信公众号文章阅读 Wemp




初二數學全等三角形 平行線順帶複習 人人焦點




最高 二等辺三角形 角度 問題 壁紙 配布




09同位角 内错角 同旁内角相交线与平行线初中数学初一 Youtube




平行線と角 図のように 平行な2直線l Mと正三角形abcがあり 直線lと辺 数学 教えて Goo



七数 专题训练三 利用平行线求角度5 哔哩哔哩 つロ干杯 Bilibili




等腰三角形的性质等腰三角形的性质
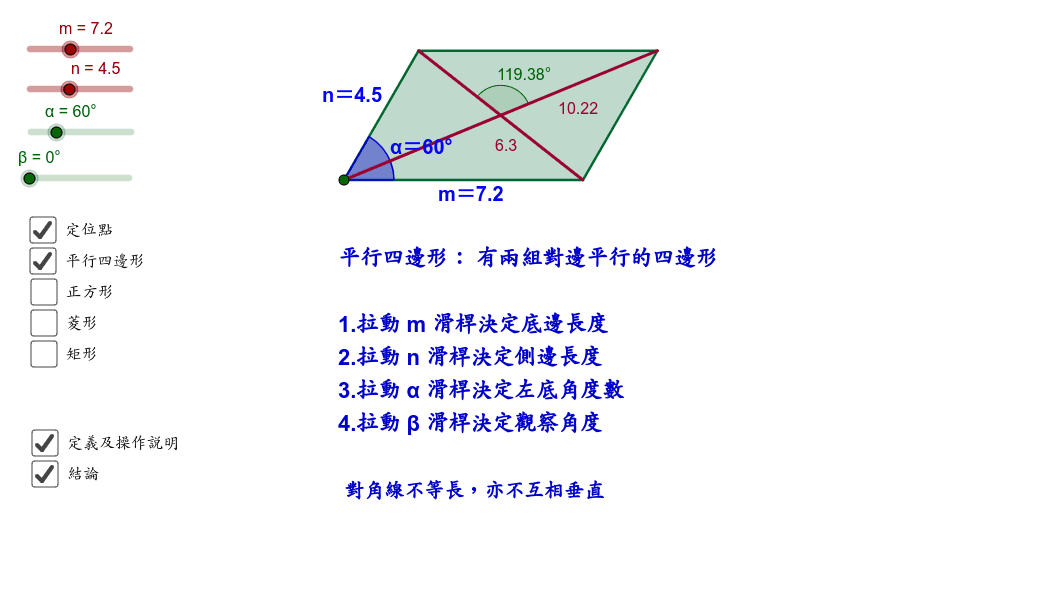



翰林數學 2下 Ch4 2 特殊平行四邊形有關對角線的性質 Geogebra



初中數學 梯形的五種常用輔助線添加方法 17道例題詳解培優幾何 雪花新闻




旋轉卡尺 Hackmd




怎么构造一条与给定直线平行的直线 通过给定点 最有妙招网
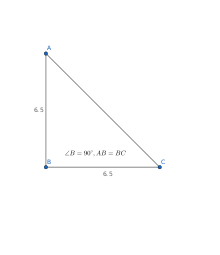



三角形 维基百科 自由的百科全书



03三角形与平行线综合三角形 2 初中数学初一 Youtube




如何找到相交线之间的角度 数学21




学生文具批发上海教材用多功能三角尺多功能尺可画平行



兩平行線中的四個角 數學謎題 Gameschool遊戲學校




現代規則幾何無縫向量模式條帶條紋的平行線抽象光學藝術設計向量圖形及更多三角形圖片 Istock



腾讯内容开放平台




两平行线间 三角形的周长和面积




数学天才罗巴切夫斯基 称平行线能相交被质疑 高斯 几何学 网易订阅



腾讯视频




什么是等分线 其定义和含义21



幾何定理



Q Tbn And9gcse0mrtmoespkkhtjstwzqae7cxfkff2uiiffagh8ii1sd0nsdu Usqp Cau




等腰三角形的性质等腰三角形的性质



用多功能三角尺画垂线与平行线 Page77 沪教版四年级数学下册电子课本 教材 教科书 好多电子课本网
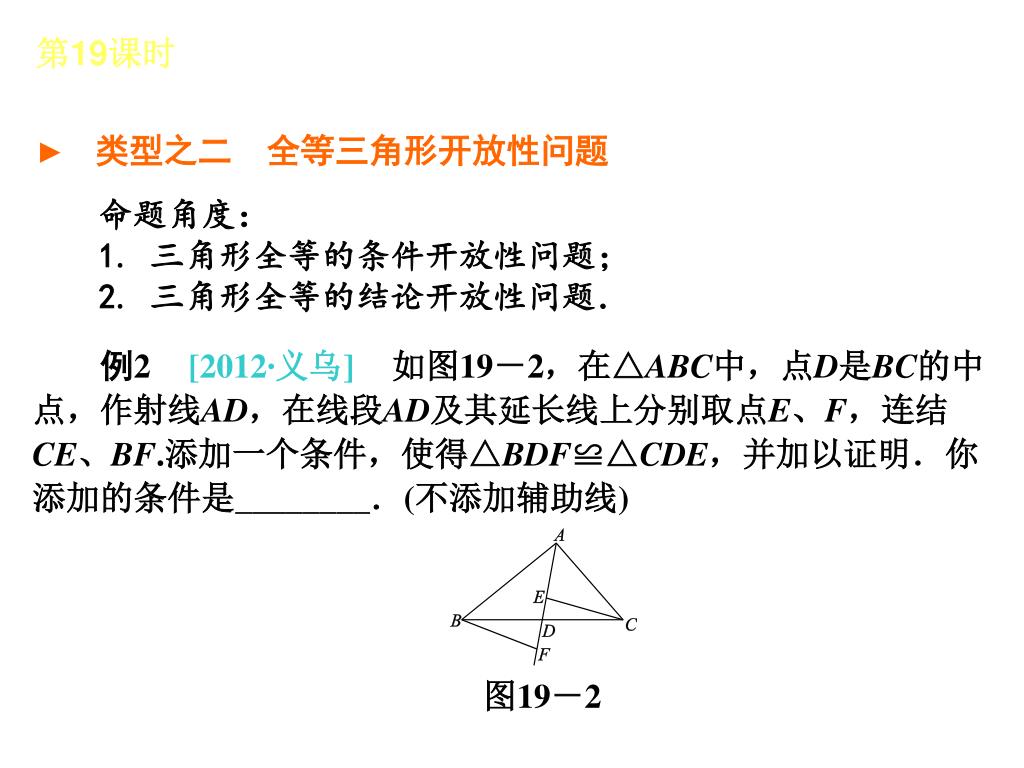



Hd限定三角形角度問題 最高のカラーリングのアイデア



七数 专题训练三 利用平行线求角度3 哔哩哔哩 つロ干杯 Bilibili



平行四边形的性质 禾教 初中数学互动课堂



四直角三角形的射影定理 人教版高中选修4 1数学电子课本 数九网




角度平行尺价格 角度平行尺图片 星期三



几何长度 角度关系沟通的桥梁自然是基本定理 定律 法则 公式



平行 维基百科 自由的百科全书



三角形内角和定理 平行线的证明ppt 第1课时 第一ppt




Ppt 第17 讲三角形与全等三角形powerpoint Presentation Id



初一数学 期末押题 角度之间的关系 专题复习 模型
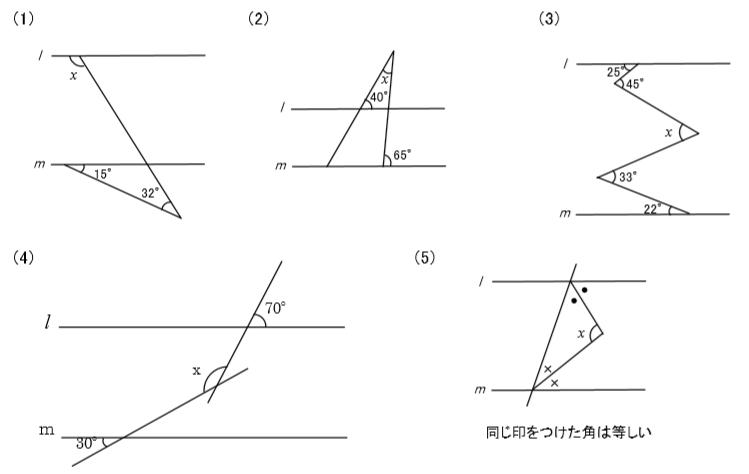



中2数学 対頂角 同位角 錯角と平行線の関係のポイントと練習問題 Pikuu



两条平行线中的三角形 已知角度 求角度 两种做法 哔哩哔哩 Bilibili



初一下册数学丨平行线性质专题 初中数学 学习资料大全 免费学习资源下载



五年级三角形求边长 西瓜视频搜索



七数 专题训练三 利用平行线求角度4 哔哩哔哩 つロ干杯 Bilibili




角度三角板 新人首单立减十元 21年8月 淘宝海外




三角形內角外角平分線夾角計算規律和規律探索 人人焦點



秒杀名师初中数学八年级上三角形与平行线综合 腾讯视频



初一下三角形旋转 西瓜视频搜索
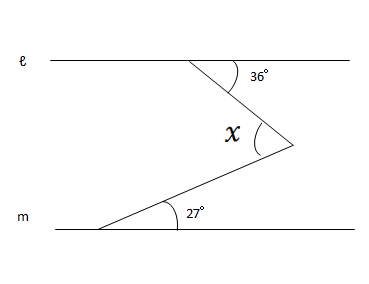



平行線と角度 6 ネット塾
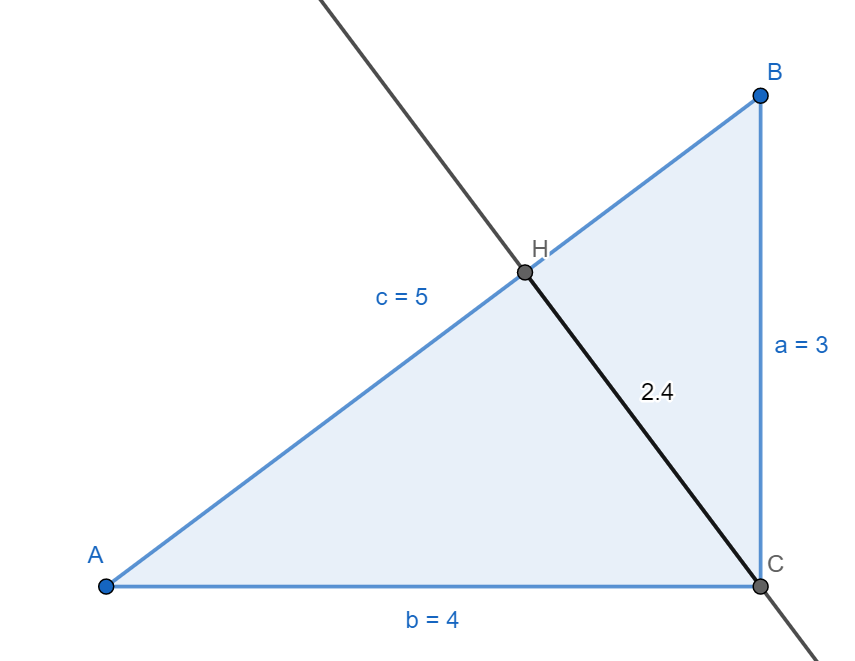



初中 彻底度量345三角形 345三角形的精确角度 精作网




中考數學 三角形中 怎麼求角度 平行及線段相等 18中考真題 每日頭條


