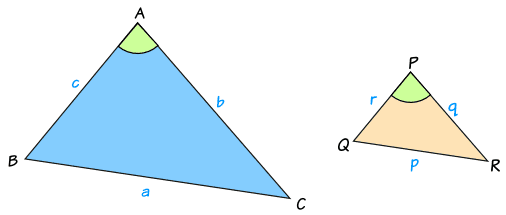
頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b関連項目:4.三角比の相互関係 まとめ2 関連項目:7.余弦定理 例題10 関連項目:6.正弦定理 例題8 adh と bch が相似形であることに着目する。 解答 ・ となる。ここで,∠abc は鈍角なので, . ・ abc について,余弦定理を用いる。 中3 三角形と比の定理の逆 中学生 数学のノート Clear 表紙 1 公開日時 18年11月28日 21時03分 更新日時 21年01月23日 14時26分 中学生 3年生 数学 相似な図形

怎么使用 相似三角形的定理 做证明题 一 百度经验
三角形 比 定理
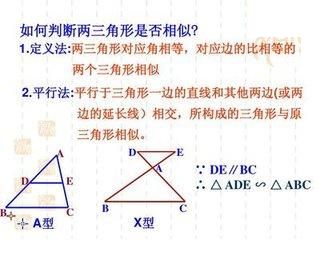
三角形 比 定理- 今回は数aの範囲から、チェバ・メネラウスの定理と三角形の面積比の問題を扱います。 チェバ・メネラウスの定理から確認していきましょう。 次に線分の比と三角形の面積比の関係を見てみよう。 「高さが同じ長さの場合、底辺の比が面積比」 右図のようなとき、 abpと acpは高さが同 sinθ cosθ tanθ の覚え方・弧度法・三角比の表まとめ」の記事も参考にしてみてください。 正弦定理 2つの視点から分かる公式の覚え方・考え方 三角形 \(ABC\) に対して、点 \(A,B,C\) の内角をそれぞれ角 \(A,B,C\) とおき 点 \(A\) の反
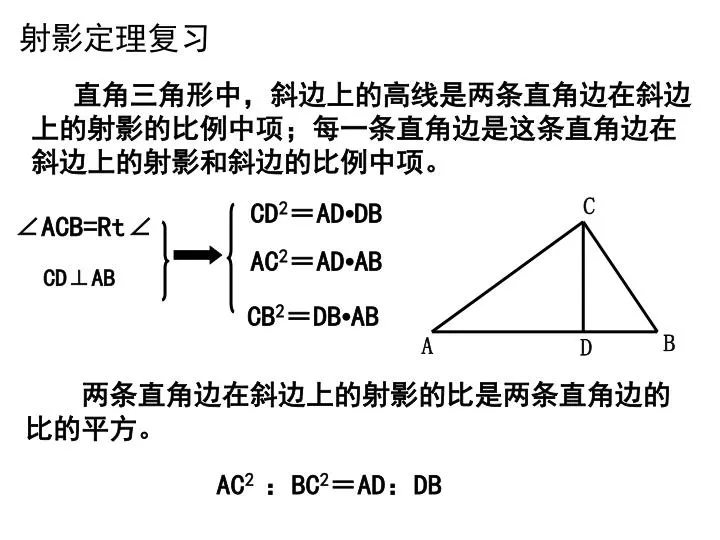



Ppt 射影定理复习powerpoint Presentation Free Download Id
三角比 三角形の解法 三角形の解法 A B C a c b A, B, C, a, b, c のうち, 3 つがわかる⇒ 他の3 つもわかる。 余弦定理 a2 = b2 c2 −2bc cosA b2 = c2 a2 −2cacosB c2 = a2 b2 −2abcosC 正弦定理 a sinA = b sinB = c sinC = 2R (R 外接円の半径) 内角の和 AB C = 180 小山哲也 電気リメディアル数学講座第6 回 6 3 2/9実際,このお題は,この3項目を順に使っていくよ。 今日は,上2つの項目を確認しながら,1.と2.を解いていこう。 三角形の角の二等分線と辺の比 \(\triangle\mbox{ABC}\) において,\(\angle\mbox{A}\) の二等分線と辺 定理:三角形 a b c abc a bc の内接円と辺 b c bc bc の接点を d d d とおく。 d d d から辺 b c bc bc と垂直な直線と内接円の交点を e e e とおく。さらに a e ae a e と b c bc bc の交点を f f f とおくとき, b d = c f bd=cf b d = cf
最後は、三角形と比の定理②から式変形を行い、「 三角形と比の定理① 」を示す方法です。 証明 三角形と比の定理②より、$$ADAB=AEAC$$三角比から三角関数の加法定理,三角形の性質へ 一高校数学での関連教材を一つの流れとして見る一 * 山口 清 Abstract A high school student studies the trigonometric ratios, the trigonometric functions and their addition theorems, and the Euclidean plane geometry in "Mathematics I, II, and A" respectively The purpose of this paper is to observe the三角形の成立条件と距離の公理 上 計量ということ 前 計量ということ 三平方の定理 美樹 数学iで「図形と計量」という単元があります. 三角比の定義を習い,三角比を用いて長さや面積,体積を求めま
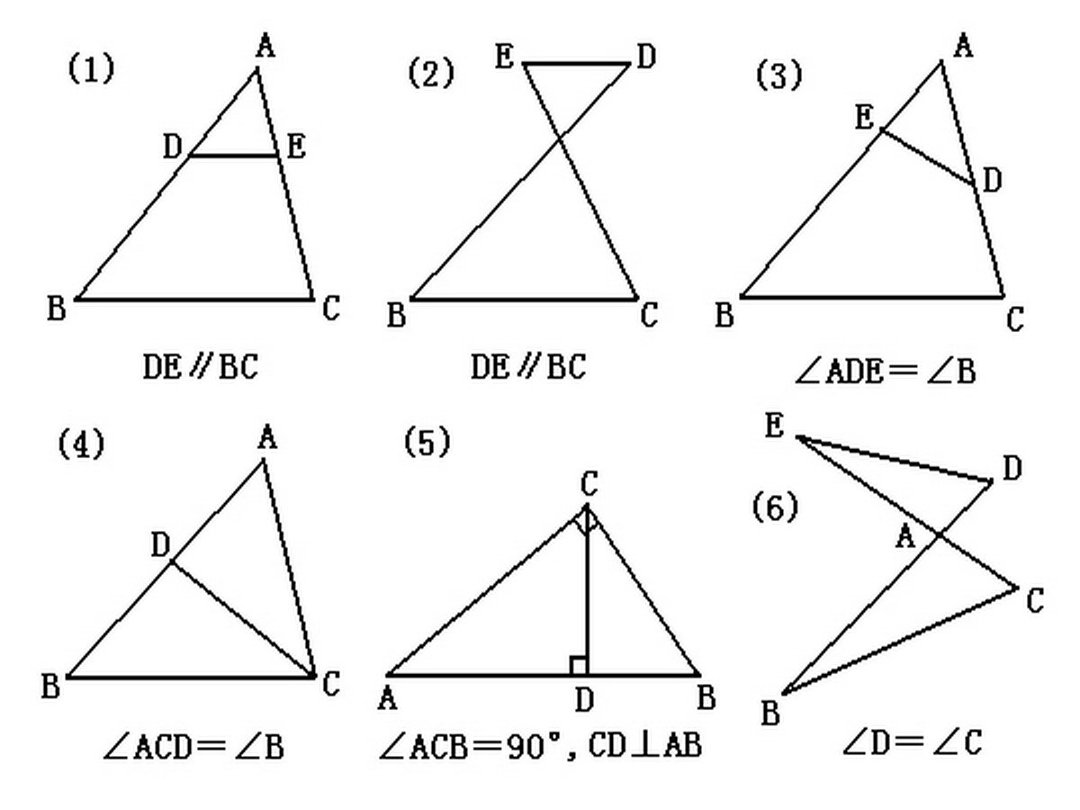
面積比と線分比とチェバの定理 まずは、面積比ってなに?ってあなたは、こちらで理解しておいてほしいんじゃ おーい、ニャンコくん、面積比と線分比の関係についての解説記事をお願い! 数学にゃんこ はーい、先生! 面積比と線分比については、基礎編と、応用編があるにゃん 基礎編 こちらは非常に有名な直角三角形です。 3つの辺の比が : : になっていれば、必ず直角三角形になります。 諸説ありますが、古代エジプトではこの形を使って直角を計り、ピラミッドを作ったのではないか、と言われているように昔から知られている形です。 整数だけで三平方の定理が成立する三辺の比のグループのことを、‟ピタゴラス数"といいます1.三角形と比の定理の逆を次のように証明した。空欄をうめなさい。 A <仮定> AD:AB=AE:AC <結論> DE//BC <証明> ( ADE )と ( ABC )で 仮定から,( AD:AB=AE:AC )-① D E




截线定理 维基百科 自由的百科全书



M 2 三角形の辺の比を求める 2 Solid Line
直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。直角二等辺三角形の底辺と高さの長さは同じです。底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります何で三角比なのに、直角じゃない三角形がでてくるの? 」って。 そこで、正弦定理が成り立つ理由を解説しておくよ。 POINT ポイントの図の、点CからABに垂線を引いて、交点をHとするよ。 ABCを、 直角三角形ACH と、 直角三角形BCH を合わせたものとして考えるんだ。 直角三角形では、 「(高さ)=(斜辺)×sinθ」 だから、 ACHにおいて、 CH=b×sinA だね。 同様にられたときに,三角 形の残りの要素を求 めることができる。 ③正弦定理・余弦定 理を三角形の決定条 件と関連付けて理解 している。 三 角 形 の 面 積 ④三角形の面積を三 角比を活用して求め ようとしている。 ④三角形の面積と辺 の長さの関係から内




三角形截距定理泰勒斯定理数学 三角形png图片素材免费下载 图片编号 Png素材网
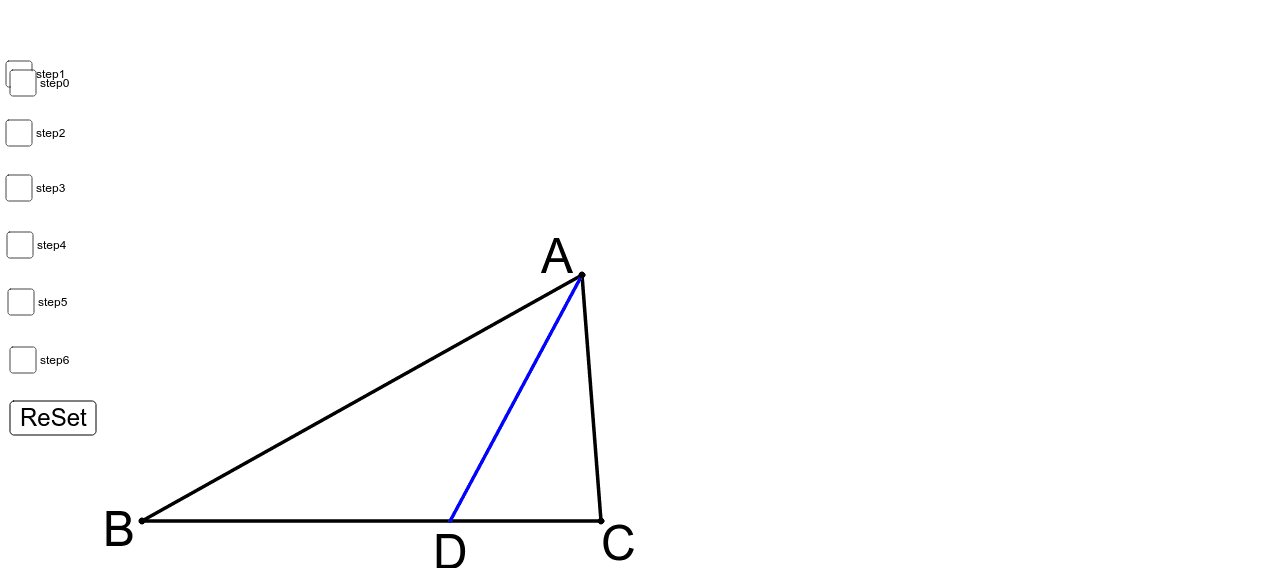



三角形と比の定理の証明1 Geogebra
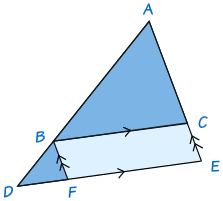
这两个相似三角形的边比例是 2:1(一个三角形的边是另一个的两个倍): 那么它们的面积呢? 如果我们多画三条线,答案就浅而易见: 我们可以看到可以有四个小三角形放在大三角形里。 因此,如果长度是两倍,面积便是四倍 面积的比是 4:1 4:1 也可以ケプラー三角形は三辺の比が等比数列となっている直角三角形で、その公比は黄金比 の平方根 であるような三角形のことである。 つまりケプラー三角形の辺の比は 、おおよそ1 :1272 :1618 である。 したがって三角形の一辺を辺とした正方形も黄金比を公比とした等比数列になる。 まとめ:直角三角形の比3つを使い倒せ! 中学数学でよく使う直角三角形の比は次の3つ。 30、60の直角三角形 45の直角三角形 3 4 5の直角三角形 これを覚えるだけで三平方の定理を使わなくてよくなるから、 だいぶラクになるね。 いきなり覚えるのは



共边定理燕尾定理 西瓜视频搜索



相似三角形定理 学习岛
つまり,比 の値は三角形の大きさに関係なく,角のみによって BCB AC 決まる値である。比 を角の正接またタンジェント(tangent) といい,tanで表す。 BC三角形と比の定理 ABC において、 点D、E をそれぞれ 辺AB、AC 上、また はその延長上の点とするとき次のことがいえる。 ①DE//BCならばAD:AB=AE:AC=DE:BC 三角比6|正弦定理の使い方を具体例から考えよう 三角比を学ぶことで正弦定理と余弦定理という三角形に関する非常に便利な定理を証明することができます. だということは容易に想像が付きますね( 余弦定理 は次の記事で扱います




勾股定理检测题 Doc 文档分享网
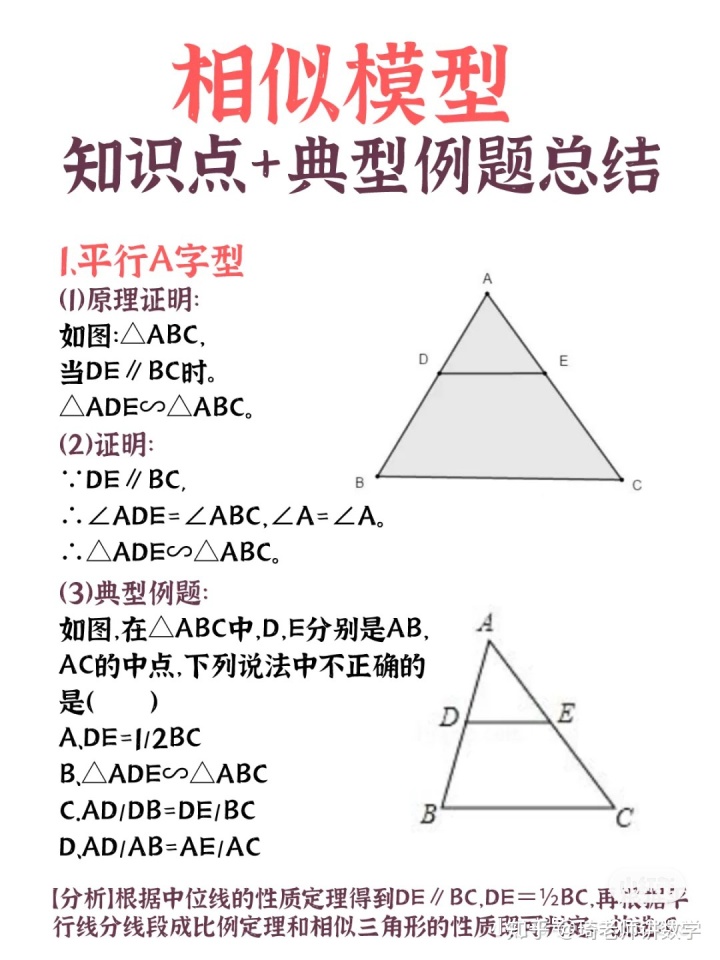



平行相似定理 初中数学 相似三角形模型合集提分收藏 阿诬123的博客 Csdn博客
角の二等分線とは、その名の通り、 ある角を二等分した線 のことです。 角を 内分 する「内角の二等分線」と、 外分 する「外角の二等分線」の 種類があります。 内角でも外角でも、 辺の比 は同じ関係式で表されます( 角の二等分線の定理 )。三角形と比の定理 A B C D E ABCの辺AB,AC上の点をそれぞれD, Eとするとき、 ①DE//BCならADAB=AEAC=DEBCである。 ②DE//BCならADDB=AEECである。 ※この定理はD, Eが辺BA, CAの延長上にあっても成り立つ。 定理の証明 4.さいごに さて今回はモーリーの定理を三角比を使って 割とゴリゴリの計算 で証明してきました。 証明の中でも何度か現れましたが「同様に」とか「 と を入れ替えれてもいい」といった議論がありました。 これは三角形の持つ「 対称性 」というもの



吴国平 中考数学几何知识重难点 相似三角形



三角形五心定律 快懂百科
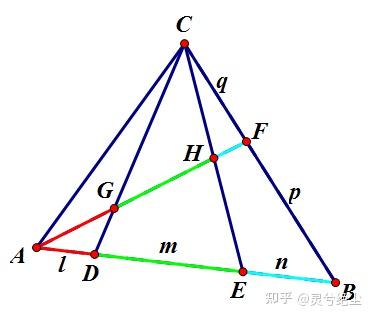
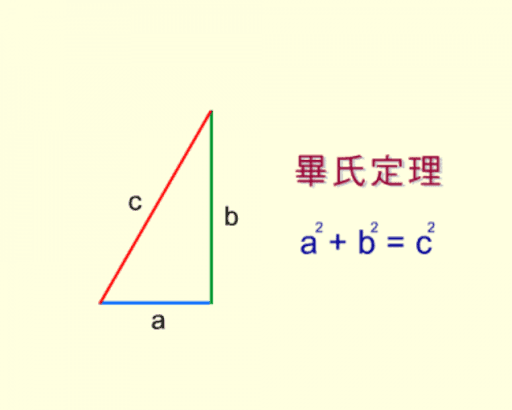
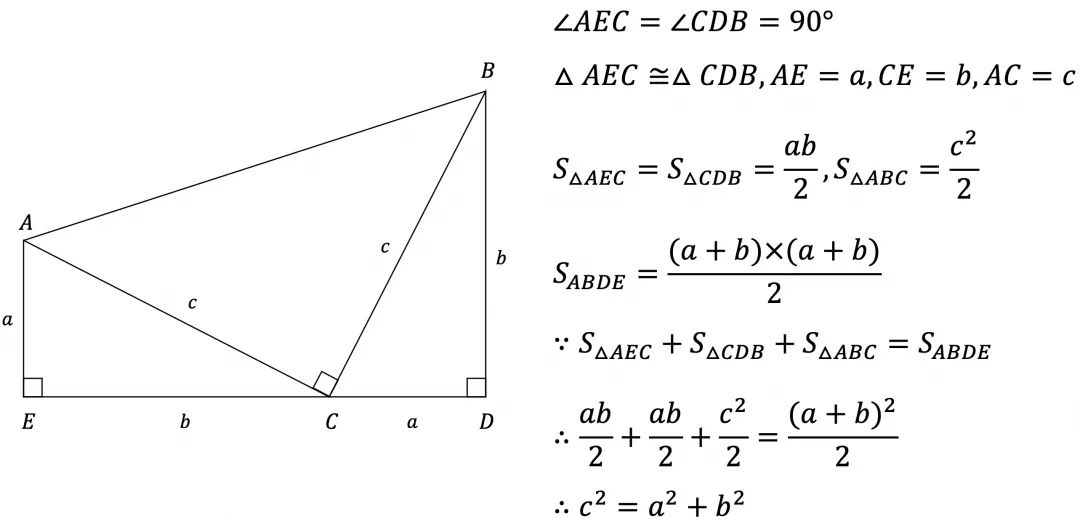
三平方の定理 直角三角形の直角を挟む 2 辺の長さを a, b とし、斜辺を c とすると、 \begin {align}\color {red} {a^2 b^2 = c^2}\end {align} が成り立つ。 3 辺のうち任意の 2 辺の長さがわかれば、三平方の定理を使って残りの 1 辺の長さを求められますね。 なお、「三平方の定理」については以下の記事でより詳しく説明しています。 三平方の定理とは?三角形と比の定理の逆 右の三角形を見てみよう。 点D、E、Fは辺ABを4等分するよう においてある。 点G、H、Iは辺ACを4等分するよう においてある。 線分DG、EH、FIは線分BCとどのよ うな関係にあるだろうか?? 結論からいってしまうと 線分DG、EH、FIは線分BCと平行に なっているんだ。 二つ三角形と比の定理の証明1 作成者 hase3desu 三角形と比の定理の証明1 新しい教材 駒東2;



射影定理 快懂百科




必杀 三角形44 与比例线段有关的几个定理共角比例定理及其证明 哔哩哔哩 Bilibili
三角形と比の定理 新しい教材 テーラー展開のズレを感じよう。 数学デッサンワークショップ用数学切り抜き帳 10月のページ では三角形の重心について次のことを知った。 三角形の重心の定理は,直観的に考えると数学以前に明らかである 重心の定理は,数学では数学の立場で証明され,力学では力学の立場で説明される 力学の立場では,三角形チェバの定理の拡張形 点Gが ABCの外にあるときも、成り立ちます。 証明1(点Gが三角形の外角の範囲内にあるとき) EFとADの交点をHとすると、チェバの定理(基本形)より、 (AB/BF)(FH/HE)(EC/CA)=1 これを三角形の面積比で表すと、 ( ABH/ BFH)( AFH/ AEH)( ECH/ CAH)=1 順番を組み替えて ( AFH/ BFH)( ABH/ CAH)(




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
三角比 ここではまず, 弧度法 という角度の表現方法について述べておくその後, 直角三角形の2辺の比を利用して 三角比 という概念を導入する 三角比は, 力の合成・分解 というものと密接に関わっており, 学校教育においても数学より先に物理で出くわす 数学 I 「図形と計量」では、三角比を学習します。 今回は、そこで登場する2大定理である 正弦定理 余弦定理 の内容と、代表的な使い方を説明していきます。




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




怎么使用 相似三角形的定理 做证明题 一 百度经验




三角形內分比 外分比定理 Easy Math Club




中国的勾三股四弦五比西方晚了多少年 网易订阅



等边三角形边长 万图壁纸网




整理版 课时作业3 相似三角形定义及判定的基本定理 下载 Word模板 爱问共享资料




內角和定理生活中的平面圖形之三角形的性質 三角形的內角 外角 內角和與外角和 Lvai



Ke Xuefuyun Com Upload Courseware Pdf




数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ



1



初中数学知识点总结 相似三角形 学习云课堂



探索三角形相似的条件 图形的相似ppt 第2课时 第一ppt
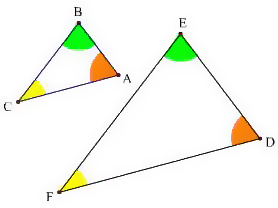



相似三角形 维基百科 自由的百科全书




Ppt 射影定理复习powerpoint Presentation Free Download Id




相似三角形模型解析 38页 鸡娃客




相似三角形相似三角形的判定和性质



初中数学 三角形 添加辅助线的规律举例1 小初高题库试卷课件教案网



三角分比问题 知乎



内角平分线定理证明 西瓜视频搜索




三角形的三等分点定理 三角形abc面积为1 Def分别为三边的三等分点 求中间小三角形面积 三人行教育网 Www 3rxing Org




相似三角形面积比和边长比的关系 快资讯




初中数学相似三角形的判定定理证明及利用三角形相似解决问题 每日头条




第二讲 三角形一边的平行线性质定理 豆知网



高中数学牛x 公式 三角形内角平分线性质定理 努力学习网



多重判定系数怎么求 北师大版九上数学4 5 相似三角形判定定理的证明知识点精讲 Yu Demon321 Mkq的博客 程序员宅基地



218几何原本第六卷 命题19 相似三角形面积的比等于相似比的平方 哔哩哔哩 つロ干杯 Bilibili



头条文章




三角形の面積比 数学の偏差値を上げて合格を目指す




怎么使用 相似三角形的定理 做证明题 一 百度经验



22 2 2相似三角形判定定理1表格式 图片欣赏中心 急不急图文 Jpjww Com



初中数学 圆幂定理与相似比 中学数学研究会 微信公众号文章阅读 Wemp




360影视 影视搜索




什么是共边定理 院勾问答




勾股定理竟然有500种证明方法 你会几种 小k算法 51cto博客




相似三角形对应边比例 相似三角形对应边成比例 这个是怎么证出来的 三人行教育网 Www 3rxing Org




11等边三角形面积公式勾股定理初中数学初二 Youtube



三角形と比




小升初数学重点 鸟头定理 每日头条



相似三角形应用举例 相似ppt课件 第一ppt



面积之比 燕尾定理模型 蝴蝶定理 梯形蝴蝶模型 共角模型 哔哩哔哩 Bilibili




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



2xj99 0godfy M



三角分比问题 知乎



相似三角形定理



斜边中线定理如何证明直角三角形斜边中线定理 不要涉及高中知识 朵拉利品网



Ml8xicmgsu7b3m




相似三角形问题解法 初中数学常用解题方法 每日头条
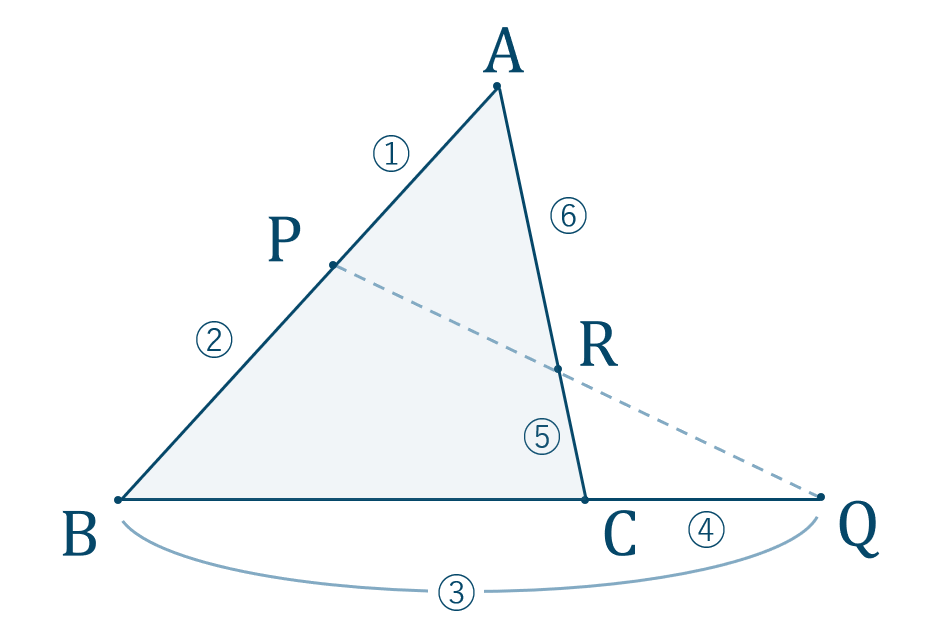



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学



几何课关于三角形你不得不记住的定理 从勾股定理到托勒密定理



1




01 相似三角形判定定理 相似三角形的定理与圆幂定理高中数学 Youtube




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
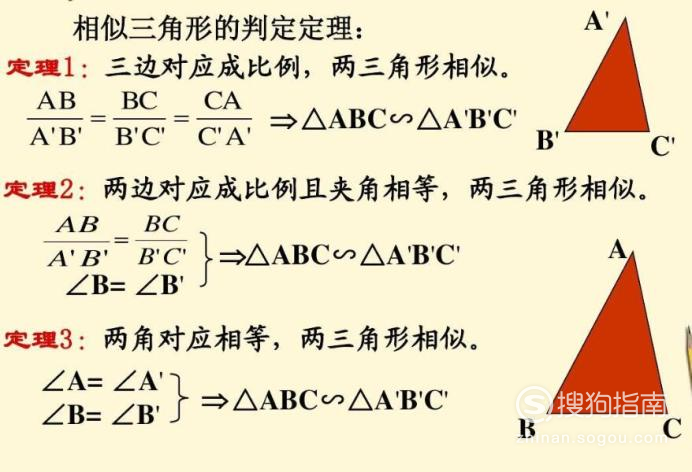



相似三角形怎么判定 搜狗指南



1



初中数学相似三角形定理归纳 史上最全就在这里



Amc10 数学中的面积公式推证
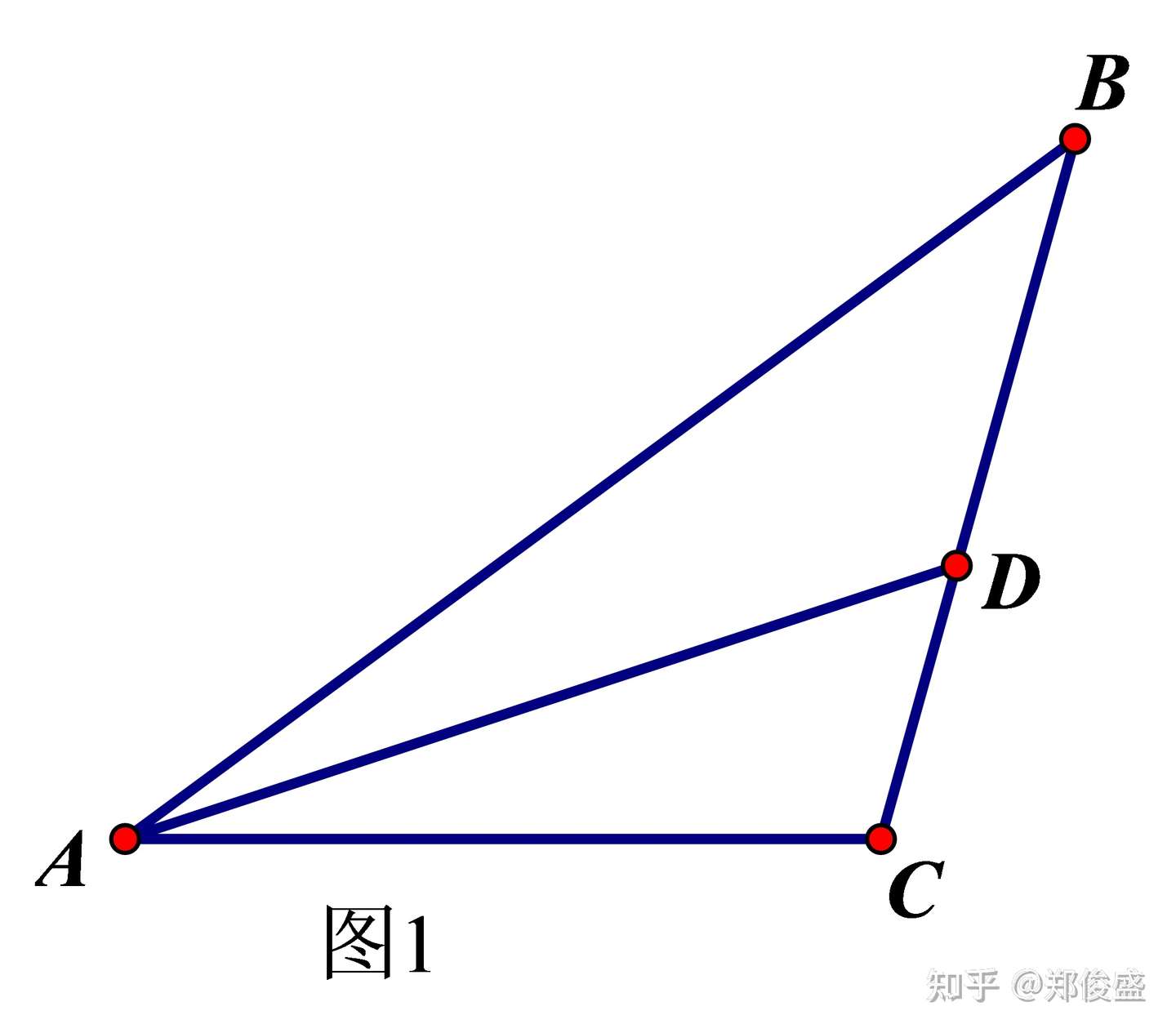



平面几何定理之六 三角形角平分线定理 知乎



三角形射影定理的统一形式及统一证明 图形




几何问题 三角形全面剖析 长方形 直角 勾股定理 正三角形 网易订阅



1




初中数学北师大版 相似三角形判定定理的证明 精品优质课ppt课件下载 Ppt 文档铺
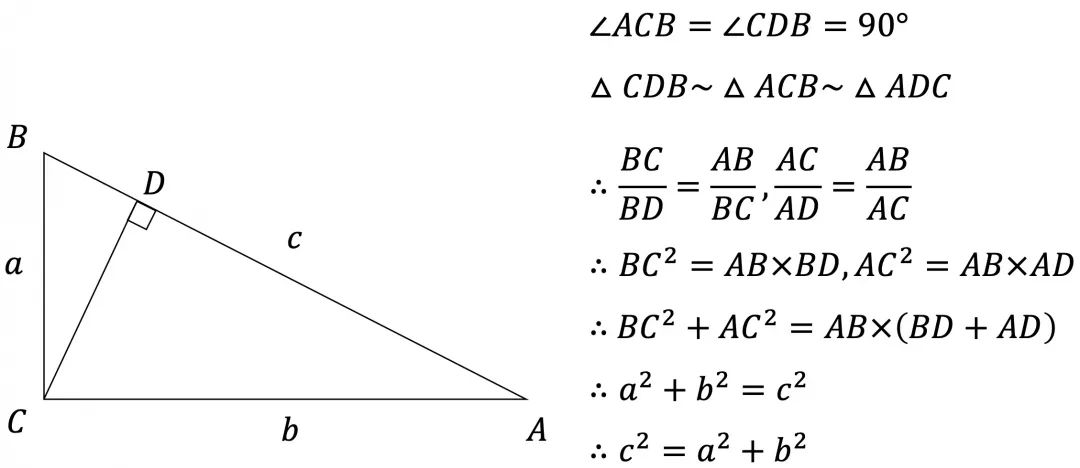



勾股定理竟然有500种证明方法 你会几种 技术圈



相似三角形专题复习 Ppt Download




三角形面积的五种典型算法 简书
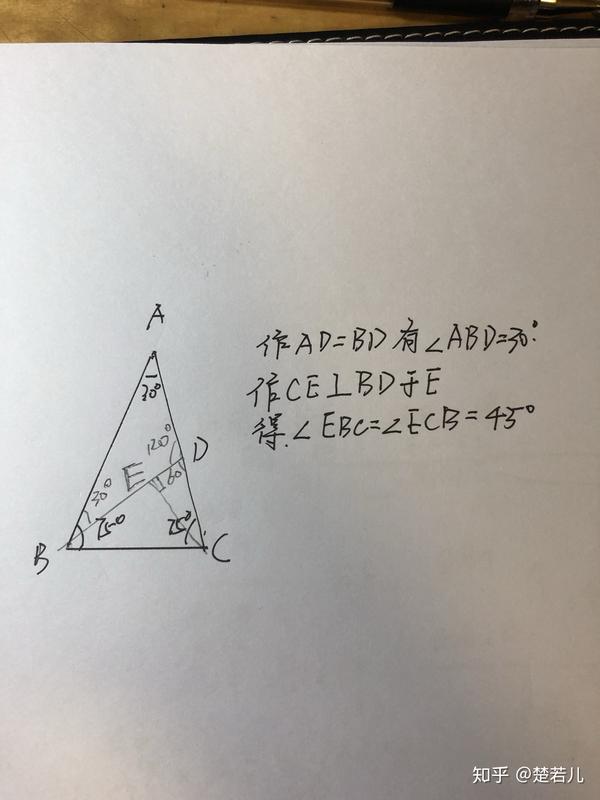



有30 75 75度角的等腰三角形 三边关系是什么 如何用勾股定理算出较简单的形式呢 30度等腰三角形三边比 圆点网



相似三角形知识点与经典题型 沃文网wodocx Com



初中数学 比例的性质 等比定理 合分比定理的证明 几何法证明 哔哩哔哩 つロ干杯 Bilibili



在三角形abc中 若a 18 B 24 A 44度 则比三角形有解吗 高三 大同辅导在线



比费马大定理还难的数 数学家证明1不是同余数 花了一千多年 快资讯




相似三角形定理的证明



勾股定理及勾股定理的逆定理 楠木轩



几何课关于三角形你不得不记住的定理 从勾股定理到托勒密定理



相似三角形判定定理 360百科



三角形外角平分线定理 初三网




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題



Amc10 数学中的面积公式推证




中学3年数学練習問題 三角形の比 辺の長さを求める問題 図形と相似



畢氏定理 勾股定理 Pythagorean Theorem Geogebra



初中幾何線段 三角形 圓等快速解題高級定理 中考的重點都在這 雪花新闻



勾股定理竟然有500种证明方法 你会几种 技术圈




正弦定理 三角形正余弦定理 环球信息网




勾股定理 西安碑林区新曙光培训学校有限公司



相似三角形定理




平面図形をマスター 三角形の面積比 応用編その3



相似知识点总结 相似知识点总结精选八篇 范文118




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




羅斯定理 粵拼 Lo 4 Si 1 Ding 6 Lei 5 係個幾何學定理 呢個定理係講喺一個大三角形內部作嘅細三角形佔大三角形嘅面積比 呢條 定理係由羅斯喺16年寫嘅書treatise




三角形中线 搜狗百科
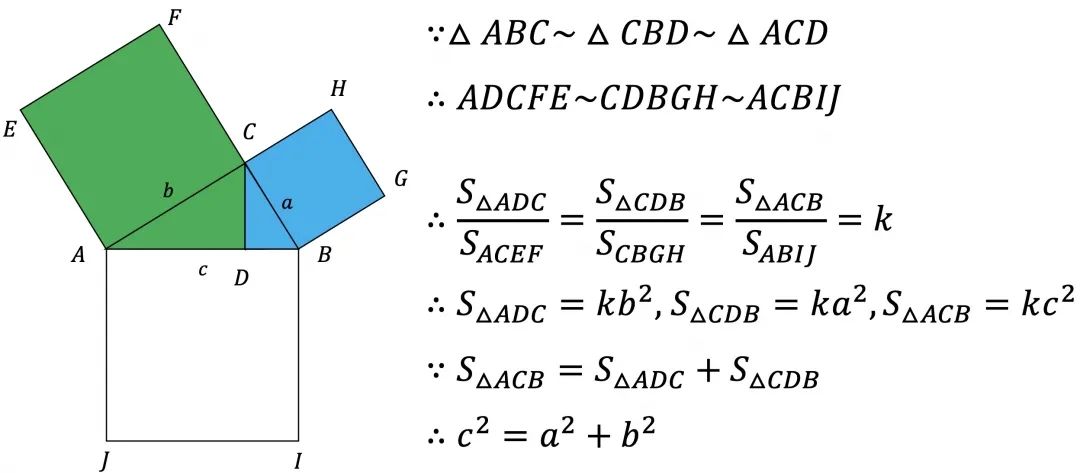



勾股定理竟然有500种证明方法 你会几种 技术圈
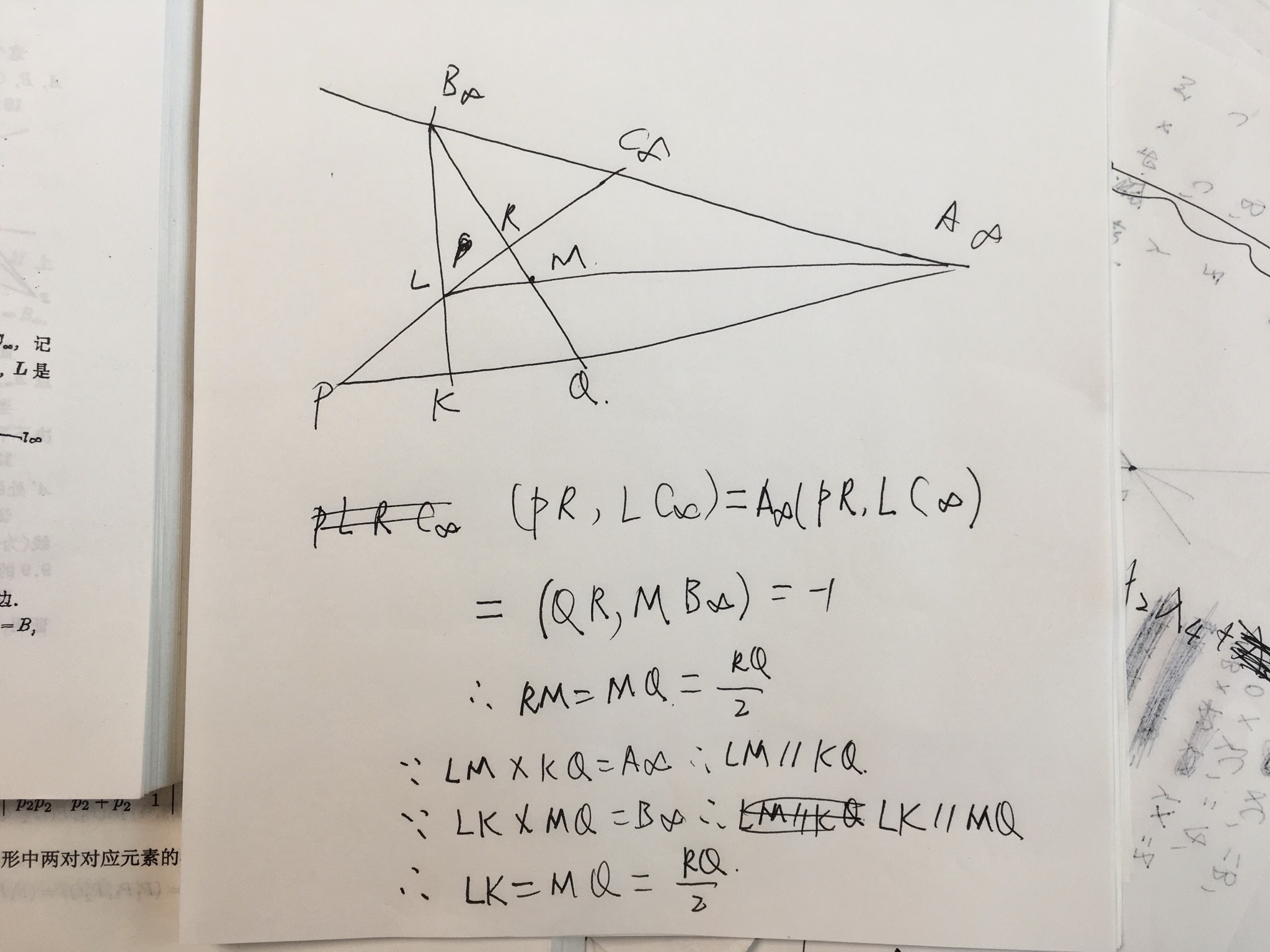



射影几何 证明三角形中位线定理后半部分三角形的中位线等于第三边的一半 Linux 0 11调试教程 程序员宅基地 程序员宅基地


