(数iiiでは,他にも∞∞など多くの型が登場しますが,数iiでは, だけです。) 不定形の極限を求めるには,分母,分子が 0 になる原因を「約分によって」取り除いてから,計算します。 「分子→0以外,分母→0以外」の分数の極限は,普通の分数です。 基本関数の極限の性質の後半で見た通り、分母・分子の極限値を使って計算ができます。では、そのまま代入できない場合はどういう場合で、そのときはどうするか。 (5回分)に加え、平成30年度試行調査を掲載しています。 正の数と負の数 22 文字複素数平面(33) 分数関数・無理関数・逆関数・合成関数(18) 2次曲線(放物線・楕円・双曲線)(24) 曲線の媒介変数表示と極座標・極方程式() 数列の極限と関数の極限(46) 微分法(基本計算パターン)(16) 微分法:頻出グラフ(陽関数表示

数学 分数関数の極限の不定形の解消のやり方とコツ 教科書より詳しい高校数学
極限 計算 分数
極限 計算 分数-差分商の極限を取る: 極限 ((xh)^5 x^5)/h, h>0 数列の極限②:無理式の極限 根号を含む$ {∞∞}$の不定形:分母や分子を有理化する} {∞} {∞}の不定形であるから,\ {分母の最高次の項で分母・分子を割る}ことになる 無理式だからといって,\ 常に有理化が有効なわけではない 重要なのは不定形を解消



3
数IIで計算できたのはn次関数の微積分だけですが、極限の計算を学ぶことによって、様々な関数の微分・積分を計算できるようになります。 まずは数IIの 微積 分を復習して、 微分 ・ 積分 の計算がどのように行われているのか、確認しておくことをお勧め 三角関数の不定形極限を機械的な計算で求める方法 三角関数の 0 0 \dfrac{0}{0} 0 0 不定形の極限を求める問題はマクローリン展開を用いた多項式近似で確実に,しかも迅速に解くことがで 数列の極限⑤:二項定理を利用する極限(r n 、n k /r n 、nr n 、r n /n!、n 1/n )と発散速度比較;
複素数の計算 (高校)虚数単位・複素数の定義(解説) 指数関数,対数関数の重要な極限,微分 簡単な重積分の計算 重積分区間が変数に依存するとき数列の極限⑦ 場合分けを要する無限等比数列r n を含む極限;複素数の基礎~複素平面と極形式・複素数値関数の微積分 定積分①定積分の定義と積分可能性の判定に関する諸定理 定積分②定積分の性質ー積分の平均値定理・微分積分学の基本定理 定積分③置換積分法と部分積分法の計算例ーウォリス(ワリス)の公式
②S n の極限を計算 の手順で求めてきましたね。特にこの問題のように分母にルートがあるときは,①の計算の際に有理化をしてS n を求めます。②の計算の結果,S n の極限が定数になるときを収束と言い,±∞のように定数とならないときは発散と言います。極限が計算されるポイントは、たとえばπ/ 4 のような数字または単純な式で指定することができます。 極限の計算は正の無限大( inf )、負の無限大( minf )と複素数の( infinity )無限大にも対応し高校数学Ⅲの勉強法のわからないを5分で解決 映像授業のTry IT (トライイット) ピックアップ映像授業 極方程式からx,yの方程式へ(1) 高校数学Ⅲ 線分の垂直二等分線の方程式 高校数学Ⅲ 無限等比級数(3) 高校数学Ⅲ 面積の計算(1)




不定形の極限の求める計算過程の誤り お世話になります グラフを書く 数学 教えて Goo




高校数学 循環小数から分数への変換 0 999 1 受験の月
数列の極限①:整式と分数式の極限 数列の極限②:無理式の極限 数列の極限③:和や積の極限 極限の条件の利用 分数式が収束するための必要条件 数列の極限④:はさみうちの原理と追い出しの原理 数列の極限⑤:二項定理を利用する極限(r n 、n k /rこの映像授業では「高校 数学Ⅲ 極限12 無限級数の計算1」が約21分で学べます。この授業のポイントは「手順1 シグマをnの式で表す数列の和の極限を定積分に直す方法 数列の和の極限を定積分に直すには,次のような図を考えます. (公式) この公式を使うには,「各部品」を正確に対応させることが大切です.(初めは,大変難しいものです.) <要点> 1 まず,Δx(通常は1/n)を
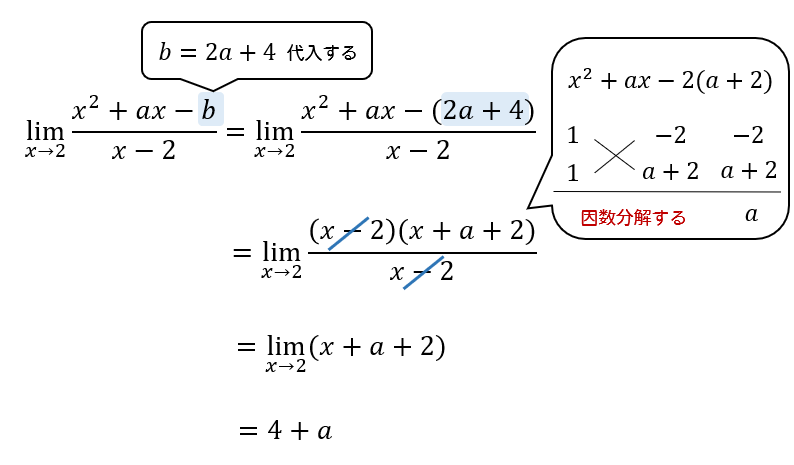



数学 極限値からの係数決定 なんで分子が0になるの 数スタ



1
定積分はリーマン和の極限値ですから,リーマン和の極限値を計算するために定積 分を用いることがあります. 例題 正の自然数を表す変数n の関数 1 n n ∑ k=1 r 4 n k3 について,ある関数のリーマ ン和であることを説明して,n → ∞ のときの極限値を数とも呼ばれる)を 例にして,そ の計算過程で生じる 極限計算の現象を分析し,そ の意義・問題点を検証す る団 でなく1/2同 を扱う理由は,xは 鱗 であ り,整 数の性質と実数としてのxの 性質とが区別し にくいからであって,1/2に 特別な意味はない。1/2x極限の考え方 さて,このような2変数の関数に対して微分や積分を考えていくのですが,1変数の微積分と同様に極限という概念が重要になってきます。 1変数の場合の微分係数の定義は,次のとおりでした。 関数 f(x) が x = a で連続であり,かつ極限値 lim h
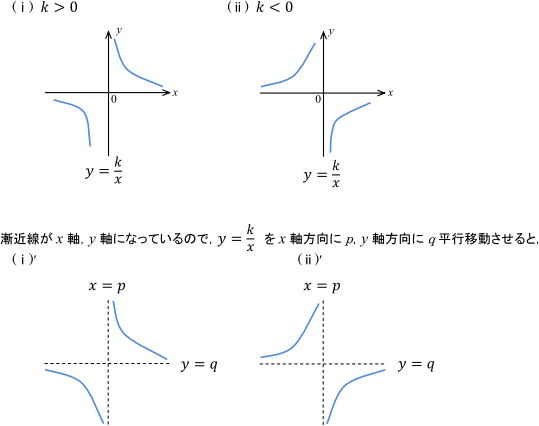



関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト




数3の数列の極限で 有利化をする問題と有利化をしない問題の違いを教 数学 教えて Goo
数学ツール 微分電卓 積分電卓 積分計算 極限の計算 級数計算機 方程式を解く 式の簡略化 因数分解 式の計算機 逆関数 テイラー級数 行列計算機 行列演算 グラフ計算機 2次元図形の求積 3次元図形の求積 素数 素因数分解 フィボナッチ数 ベルヌーイ数(※ 範囲外) 次に逆関数が存在する条件について考えてみよう。逆関数も関数であるから(逆関数の)定義域に含まれるすべての で () が一意に定まらなくてはならない。 すなわち、 = において、定義域の と値域の のどちらかを定めるともう片方が一意に定まるような関数でなくてはならない。 クイズ付き (14) 数a 場合の数と確率 (21) 数a 平面図形 (11) 数a 整数 (21) 数b ベクトル (40) 数b 数列 (23) 数iii 2次曲線 (8) 数iii 分数関数など (7) 数iii 微分(基本計算と基本グラフ) (8) 数iii 微分の応用 (13) 数iii 極限 (16) 数iii 積分の応用 (25) 数iii 積分計算 (17) 数iii




数列の極限に関する知識まとめ 理系ラボ



1
その計算のしやすさから、コンピュータによる数 値計算が実用的である。 限回の除算をすればよいことになる。有限の連分 数は有理数しか表せないのに対し、無限にすれば して、その極限無限等比数列r n 、ar n の収束条件;上の説明では,関数の極限 lim x → af(x) を考えるために,実際に x の値を a に近づけて計算するという方法をとりました。 それでは,関数の極限は,コンピュータや電卓の力を借りなければ求められないかというと,必ずしも,そうではありません




Xlogxの極限 大学入試によく出る極限の問題 大学入試数学の考え方と解法




関数の極限計算をしてみる その4 無限大に飛ばす極限 編 高校数学の知識庫
これまでの計算で,収束する数列を連続関数(逆数やべき乗など)に代⼊した場合の極限, 収束する⼆つの数列の積の収束など,対応する値に収束することは証明せずに,計算をしてい ますが,これらはすべて正しく,厳密な証明が可能です。 を⽤いて計算極限計算コツ, 数列の極限について|数学|苦手解決q&a|進研ゼミ 解説 極限を求める式は,例えば,と書きますが,xは1という値そのものになるのではなく,あくまでも,xを1に限りなく近づけたら,x+3は4に限りなく近づく,つまり,x →1のとき,x+3部分分数分解と級数の極限 高校数学.発展的話題まで. 一つの例 まず,はじめに次の級数(数列の和のこと)を求める. ∑n k=1 1 k(k1) これは,以下のように式変形を行えば,求めることが出来る. ∑n k=1 1 k(k1) = ∑n k=1 (1 k 1 k1) = 1 1 n1 (= n n1) このこと



関数の極限の範囲です 4 が分母が0になっているのですが それをど Yahoo 知恵袋




極限公式一覧 極限のイメージから基礎問題 重要テクニックまで総まとめ 青春マスマティック
Subscribe 高校 数学Ⅲ 極限10 漸化式と極限 (22分) Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computerから4つの数列の極限を求める問題である。このあたりは、高校数学の範囲内であろう。指数の計算に熟知して おく必要があると思う。 (追記) 1.昨日の一風景 (1) 作日の15日(日)の朝8時から用水路の掃除があった。日から水を田に引くことになる。部分分数を扱った計算では、分母が、n(n1)のように、 隣り合う2数の積 であることが多いのが特徴です。 このような分母であれば、一般に、 小さい数を前の分数式 に、 大きい数を後ろの分数式 にして分解します。 部分分数に




ロピタルの定理 Wikipedia




Lim 1 X 無限大となります 分母が0のときの極限の求め方を解説しました Youtube
数列 { a n } が「有限確定」の値に収束しないときは 発散する といいます. 正の無限大(∞)は特定の数字ではありませんが,正の無限大に発散するときも極限があるといいます. 負の無限大(−∞)に発散するときも同様に,極限があるといいます



Studydoctor右側極限 左側極限とは 高校数学 Studydoctor




高校数学 片側からの極限 1 問題編1 映像授業のtry It トライイット



数列や級数の極限 京極一樹の数学塾




極限の考え方を知ろう Lim リミット って一体なに




極限値の問題 高校レベル 極限値の問題です回答よろしくお願いいた 数学 教えて Goo




基本 分数関数の極限 なかけんの数学ノート




導関数dy Dxのdyとdxを説明するのは実は苦労



3




ネピア数eに関連したいろいろな数列の極限値を求めてみよう 身勝手な主張




極限の定義 公式 計算問題の解き方 高校数学 Irohabook




ロピタルの定理 Wikipedia



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典




数列の極限に関する知識まとめ 理系ラボ




指数関数の極限と爆発性 高校数学の美しい物語




数学 関数の極限チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru



極限の計算なのですが 途中式の分数の部分がわからないです Limt B T2 Yahoo 知恵袋



Http Www Naka H Ibk Ed Jp Action Common Download Main Upload Id 2326




式変形による極限の解法まとめ 大学受験数学の解き方




数列の極限に関する知識まとめ 理系ラボ



極限値の計算問題 京極一樹の数学塾




極限の問題が解けません 極限と言っても分数のところです Lim X Okwave




極限を計算する 極限を計算する とは 意味 英語の例文



0はなぜ出来ないのか 極限までわかりやすく解説




極限値の求め方 不定形を含む問題も数学 の範囲で解く方法




15 1846号 計算装置及びプログラム Astamuse




数列の極限の求め方その1 分数式 有理化 数学の偏差値を上げて合格を目指す



1




分母が0に近づくときの極限の求め方 高校数学の勉強法 河見賢司のサイト




微分係数の極限値を求める時に分数の形ではカッコをつけないのにlim A B などの形 Clear




1 と 4 を分数の形にしているのはどういう事ですか 1 3 とは違い 2 Clear




数列の極限の求め方その4 漸化式で与えられた場合 数学の偏差値を上げて合格を目指す




数学3の関数と極限についてです Clear




高校数学 関数の極限の基本 3 問題編 映像授業のtry It トライイット




極限って何 極限のその先へ 高校数学なんちな




基本 対数関数の極限 なかけんの数学ノート




0 極限値0の意味と極限の不定形を確認 無限大 無限小 後編 数学 極限 そーまのブログ屋さん




15 1846号 計算装置及びプログラム Astamuse




不定形の極限の求め方と関数の極限公式をわかりやすく説明しました



極限値の計算問題 京極一樹の数学塾
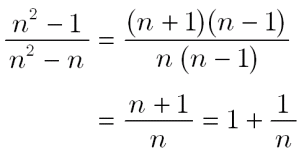



数列 極限値の求め方 大人が学び直す数学



関数の極限 分数がゼロがいい時とダメな時の違いはなんですか Yahoo 知恵袋



誤答から学ぼうシリーズ 無理式と極限 ほのぼの数学頑張ろう
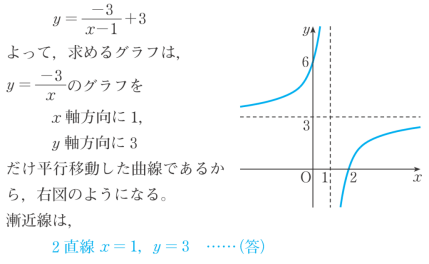



関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典




ロピタルの定理 Wikipedia




15 1846号 計算装置及びプログラム Astamuse




負の無限大への極限対策 怜悧玲瓏 高校数学を天空から俯瞰する
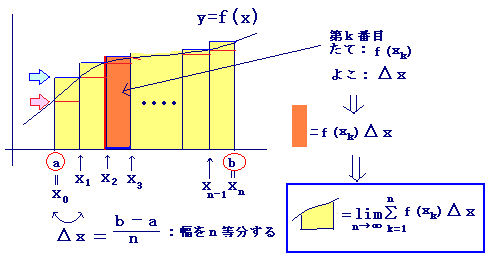



Lims 区分求積法



数学の計算やグラフを自動で Desmos が便利すぎる ねこみみめいど



数学の極限について質問なのですが下の画像の問題の極限のやり方は Yahoo 知恵袋




極限の定義 公式 計算問題の解き方 高校数学 Irohabook



数列や級数の極限 京極一樹の数学塾



極限値の計算問題 京極一樹の数学塾




不定形の極限値をロピタルの定理で求める例 微分積分学 タロウ岩井の数学と英語 Note



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典



関数の極限のちょっとした小手技



数学iiiチェック リピート 第3章 2数列の極限 12 分数漸化式と極限 Pukiwiki




高校数学 数列の極限 無理式の極限 受験の月



極限にかんすることなのですが 分数の極限を求める時に有理化してから求める時とし Yahoo 知恵袋




高校数学 三角関数の極限 4 問題編 映像授業のtry It トライイット



極限値の計算問題 京極一樹の数学塾



48s96ub7b0z5f Net Mugenkyuusuu



数学iiiチェック リピート 第3章 2数列の極限 13 漸化式とハサミウチの原理 Pukiwiki




極限の定義 公式 計算問題の解き方 高校数学 Irohabook




数学 分数関数の極限の不定形の解消のやり方とコツ 教科書より詳しい高校数学




数列の極限に関する知識まとめ 理系ラボ



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典




極限の定義 公式 計算問題の解き方 高校数学 Irohabook




極限の定義 公式 計算問題の解き方 高校数学 Irohabook




三角関数の不定形極限を機械的な計算で求める方法 高校数学の美しい物語
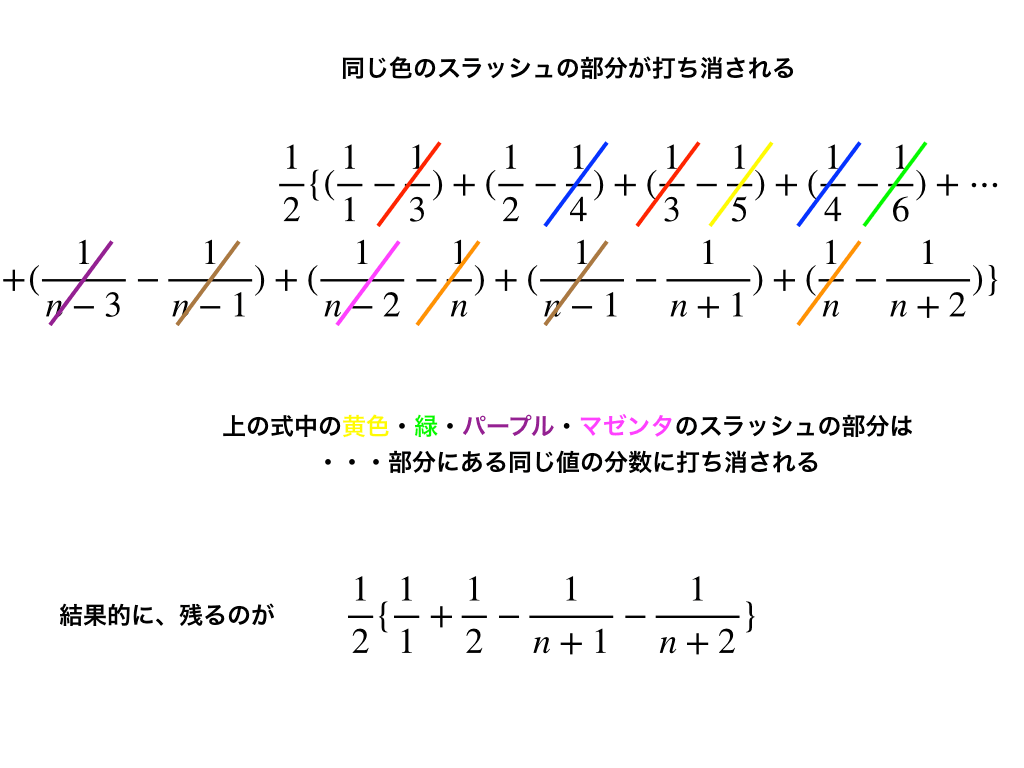



部分分数分解のやり方のコツ 公式と応用までわかりやすく解説




高校数学 極限の条件の利用 受験の月




指数関数 対数関数 多項式の発散速度について 工業大学生ももやまのうさぎ塾




数学 極限値からの係数決定 なんで分子が0になるの 数スタ




数学 部分分数分解 すると 極限 を求めることができるよ 高校数学 数3 極限 行間 ぎょうのあいだ 先生




無限級数 おいしい数学




高校 数学 極限22 極限の計算1 18分 Youtube




高校数学 関数の極限 多項式関数と分数関数の極限 受験の月




添削課題 数列の極限 部分分数分解 数 1対1対応演習 Matsu Math Note




高校数学 関数の極限の基本 3 問題編 映像授業のtry It トライイット



極限とは 公式一覧や極限計算のポイントをわかりやすく解説 受験辞典




ロピタルの定理の条件と例題 高校数学の美しい物語




ルートの極限 と応用公式 不定形でわかる有理化を使うポイントと効率的な解法 青春マスマティック
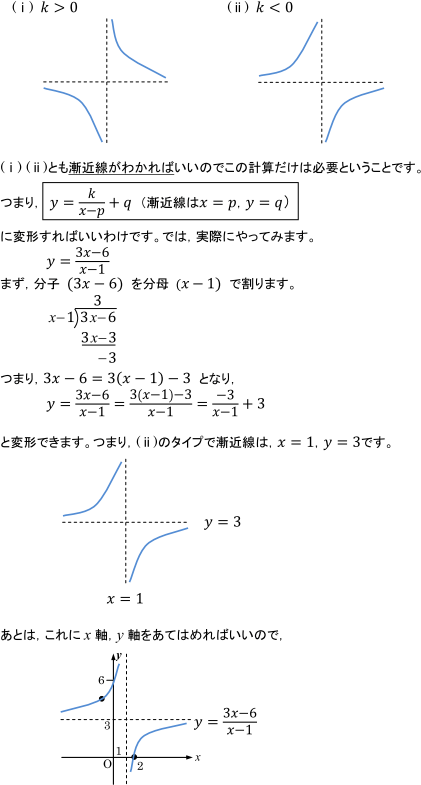



関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト




数列の極限の分数の形が出てきたら分母のnの最高次で分子と分母をわるんだと思っていたの Clear




極限の問題における 逆に の説明について Okwave




数列の極限について 数学 苦手解決q A 進研ゼミ高校講座



極限値 数iiの不定形の極限




数3の極限の問題です 解答だけでわかりにくいかもしれませんがお願い 数学 教えて Goo




極限の定義 公式 計算問題の解き方 高校数学 Irohabook


